Généalogie de la famille DUCOS - PONTET

Généralités sur les implexes

Les implexes : mode d'emploi

 

Un petit calcul...

Livrons-nous d'abord à un petit calcul amusant. Nous avons chacun 2 parents, 4 grands-parents, 8 arrière-grands-parents, 16 arrière-arrière-grands-parents, etc... Le nombre de nos ancêtres est exponentiel, multiplié par 2 à chaque génération.

Bon, jusqu'ici, tout va bien...

Imaginons qu'on remonte à la 40ème génération. En partant de l'hypothèse qu'il y a 25 ans entre chaque génération, cela nous fait remonter 1000 ans en arrière, c'est-à-dire vers l'an 1000.

A la 40ème génération, le nombre de nos ancêtres vivant à cette époque est :

2x2x2x2x2x2x2...x2 (trente-neuf fois) = 2 39 = 549 755 813 888

soit près de 550 milliards d'ancêtres vivant en France vers l'an Mil, époque où notre pays ne comptait que 10 millions d'habitants... Cela n'est évidemment pas possible !

 

Comment expliquer ce paradoxe ?

L'explication est très simple. Le nombre d'ancêtres que nous avons calculé ci-dessus est le nombre d'ancêtres théoriques. En réalité, un très grand nombre de ces ancêtres se retrouvent plusieurs fois (et même plusieurs milliers de fois) dans notre arbre généalogique, et ce pour chacun d'entre nous.

Effectivement, lors d'un mariage les futurs époux sont censés ne pas être de la même famille. Mais qui aurait pu se souvenir, lors d'un mariage célébré en 1800, que le futur époux et la future épouse avaient un ancêtre commun à la fin du XIVème siècle ? Evidemment personne... Et pourtant, deux personnes ont toujours des ancêtres communs, plus ou moins lointains !

Et cette situation donnée là en exemple, s'est produite un grand nombre de fois dans chaque famille, et ce dans toutes les familles ! Ceci semble logique, du fait que les gens se déplaçaient très peu avant la fin du XIXème siècle. C'est ce qui explique pourquoi on dit souvent que nous descendons tous de Charlemagne... et que nous sommes tous cousins !

De ces mariages, qui je le répète se retrouvent des milliers de fois dans toutes les familles, résultent que le nombre d'ancêtres théoriques est très supérieur au nombre d'ancêtres réels. Les personnages qui se retrouvent ainsi plusieurs fois dans l'arbre généalogique sont appelés des "implexes". Ils sont censés être des ancêtres différents (en théorie), mais en fait il s'agit de la même personne (en réalité). Ces implexes n'ont donc pas un seul numéro Sosa, mais 2, voire plus. Bien sûr, si un aïeul est un implexe, alors ses parents, ses grands-parents et toute son ascendance, le sont aussi !

Ne paniquez donc pas si vous découvrez un ou plusieurs cas d'implexes dans votre généalogie ! Il est tout-à-fait normal et logique que vous en trouviez. Pas d'affolement inutile donc concernant la consanguinité et ses dangers si elle est répétée sur plusieurs générations, il n'est absolument pas question de cela !

Vous trouverez un cas d'implexes au XVIIème siècle à la page Nos implexes ou bien dans l'Arbre des implexes.

 

Le taux d'implexe

Le taux d'implexe est une formule mathématique exprimant le rapport entre le nombre d'ancêtres théoriques et le nombre d'ancêtres réels. Il se calcule pour chaque génération.

Comme disaient nos professeurs de maths, soient les données suivantes :

Alors le taux d'implexe = ( T - R ) / T

Pour que ce calcul corresponde à une réalité, il faut évidemment avoir retrouvé tous les ancêtres composant cette génération n pour être sûr de connaître le nombre d'ancêtres réels.

S'il n'y a pas d'implexe, le nombre d'ancêtres réels est égal au nombre d'ancêtres théoriques, et l'implexe est nul. A l'inverse, les enfants dont les parents sont cousins germains ont un implexe d'au moins 0,5, soit 50 %.

 

Le record absolu

On cite souvent le cas du 41ème roi d'Espagne, Alphonse XIII (1886-1941). A la 11ème génération, ce souverain n'avait que 111 ancêtres différents, au lieu des 2 10 = 1024 ancêtres théoriques. Il avait donc un implexe de (1024 - 111) / 1024 = 89 % ! Qui dit mieux ?

 

Qu'en est-il dans notre généalogie ?

Pour savoir ce qu'il en est dans le cas de notre famille, je vous invite à aller sur la page Les implexes dans notre généalogie. Vous y trouverez des cas précis et concrets d'implexes dans une généalogie familiale, et un mode opératoire pour les repérer afin de pouvoir l'adapter sur votre généalogie. Encore une fois, il ne s'agit pas d'une méthode académique, testée et approuvée par les plus grands pontes de la discipline ! Il ne s'agit que du modus operandi que j'ai défini et exécuté afin d'atteindre mon but. Le Livre d'Or est à votre disposition pour vous exprimer sur la méthode utilisée.

 

Mathématiques et aspirine

Qui dit implexes dit calculs nombreux pour définir le taux d'implexe et comprendre les tenants et aboutissants de ces situations si particulières. Le paragraphe que je vous propose ne va pas plaire à tout le monde, car il fait appel à des notions mathématiques, assez simples tout de même, mais différentes selon les contextes rencontrés. Ceux qui ont fait l'impasse en maths pour le bac peuvent quand même suivre, mais attention aux maux de tête !

Le but est d'étudier plusieurs cas d'implexes qu'on peut rencontrer, nous tous dans notre généalogie, d'en comprendre les mécanismes et leurs conséquences. J'emploie dans ces lignes la notion de génération G, ou plus simplement GenG, qui indique la génération où se situent les premiers implexes rencontrés dans chaque cas. Attention, je parle bien de la génération des premiers implexes, pas de celle des enfants, frères et soeurs, dont plusieurs sont des ancêtres : les enfants ancêtres sont à la GenG-1, les parents implexes sont à la GenG. Si un ancêtre est un implexe, automatiquement ses parents le sont aussi, ainsi que ses grands-parents, etc... La GenG est donc la génération du premier implexe rencontré, la GenG+1 (la génération suivante) est celle de ses parents, la GenG+2 celle de ses grands-parents, etc... Cette précision faite, étudions d'abord 4 cas simples.

Cas simple n°1 : implexage avec décalage d'une génération dans la fratrie

Mais oui, c'est un cas simple ! Prenons le cas où 2 frères (ou 2 sœurs, ou un frère et une sœur, peu importe), sont tous les deux un ancêtre, mais ne se trouvent pas sur la même génération par rapport à leur descendant commun. Par exemple ici, le Sosa 2 et le 6 sont frères, ils ont tous les deux pour parents le 4/12 et la 5/13. Pourtant, ils ne sont pas sur la même génération par rapport au Sosa 1 : le 2 est son père, et le 6 est son grand-père maternel. Les 2 implexes sont de la GenG (ici la Gen2, la génération 2 à partir du de cujus) et ils comptent en tant que tels (ils comptent chacun 1 fois même s'ils ont 2 numéros Sosa). Même s'ils sont de la Gen3 par l'autre côté, on doit quand même les considérer de la Gen2 par le chemin le plus court.

Par contre, à la génération au-dessus qui est la Gen3 (GenG+1), on a les 4 parents des 2 implexes de la Gen2 (implexes eux aussi, 2 sosas : 8/24, 9/25, 10/26 et 11/27), qui prennent la place de 6 individus : les parents eux-mêmes plus les 2 implexes qui se trouvent à la Gen2 (12 et 13). En réalité, ce sont les 2 implexes de la Gen2 (le 4/12 et la 5/13) qui manquent à la Gen3.

Pour ce cas et ceux qui suivront, les exemples présentés ne le sont que pour constater les conséquences d'une situation d'implexe au niveau des individus manquants dans les générations précédentes. Ici, le grand-père paternel serait le fils des grands-parents maternels, ce qui n'arrive jamais ! Les cas sont en réalité bien plus espacés dans le temps, de près d'une dizaine de générations, mais il serait impossible d'expliquer la situation avec autant d'écart. Ce sont donc des exemples réduits à des écarts de générations très faibles, non pour illustrer une réalité (qui n'existe pas), mais pour expliquer un principe de la façon la plus simple possible.

 

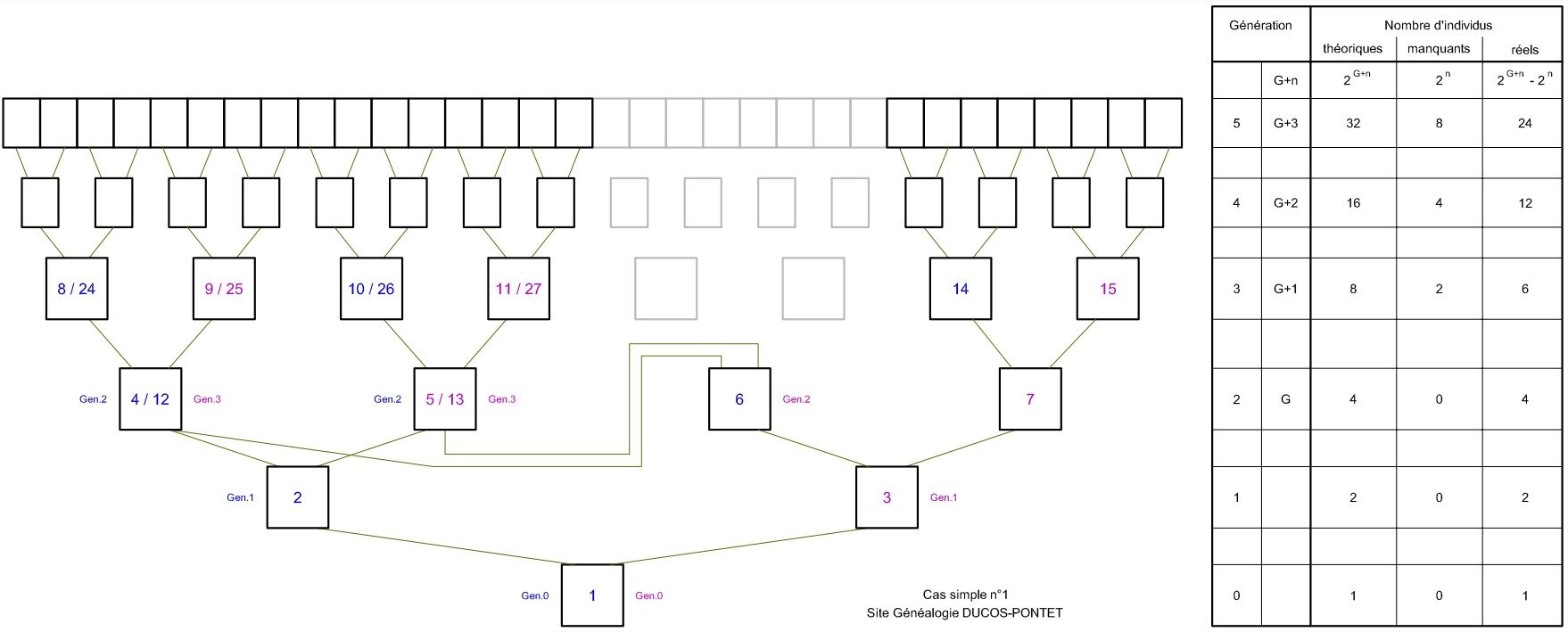
Implexe 1

Résultats constatés :

  • la Gen2 (G) est complète, et la Gen3 (G+1) a 2 individus de moins. Si on compte à la GenG+2, on en a 4 de moins. A la GenG+3, on en a 8 de moins. Les manquants doublent à chaque génération.
  • Si on a un implexe à la génération G d'un côté et à la génération G+1 de l'autre, alors la GenG est complète (2 G), la GenG+1 compte 2 individus de moins (2 G+1 -2).

Conclusions :

  • A la GenG+n, on a 2 n (2 puissance n) manquants.
  • La GenG+n compte donc (2 G+n - 2 n) individus. Ceci ne fonctionne pas pour la GenG, pour laquelle n = 0, puisque 2 0 = 1 alors qu'on a 0 manquant. Mais la formule est correcte pour toutes valeurs de n > 0 . Ceci sera valable pour tous les cas que nous allons voir.

Cas concrets dans notre généalogie :

Cas simple n°2 : implexage sur 1 seule personne (mariée 2 fois, chaque conjoint est un ancêtre) avec décalage d'une génération dans la fratrie :

Reprenons le cas précédent, mais au lieu d'avoir 2 implexes à Gen2, on n'en a qu'un. Ici, le sosa 2 et le sosa 6 n'ont que leur père en commun, leurs mères sont différentes. Donc à Gen3, il manque 1 seul ancêtre (l'implexe lui-même), à Gen4 il en manque 2, à Gen5 il en manque 4, etc…

 

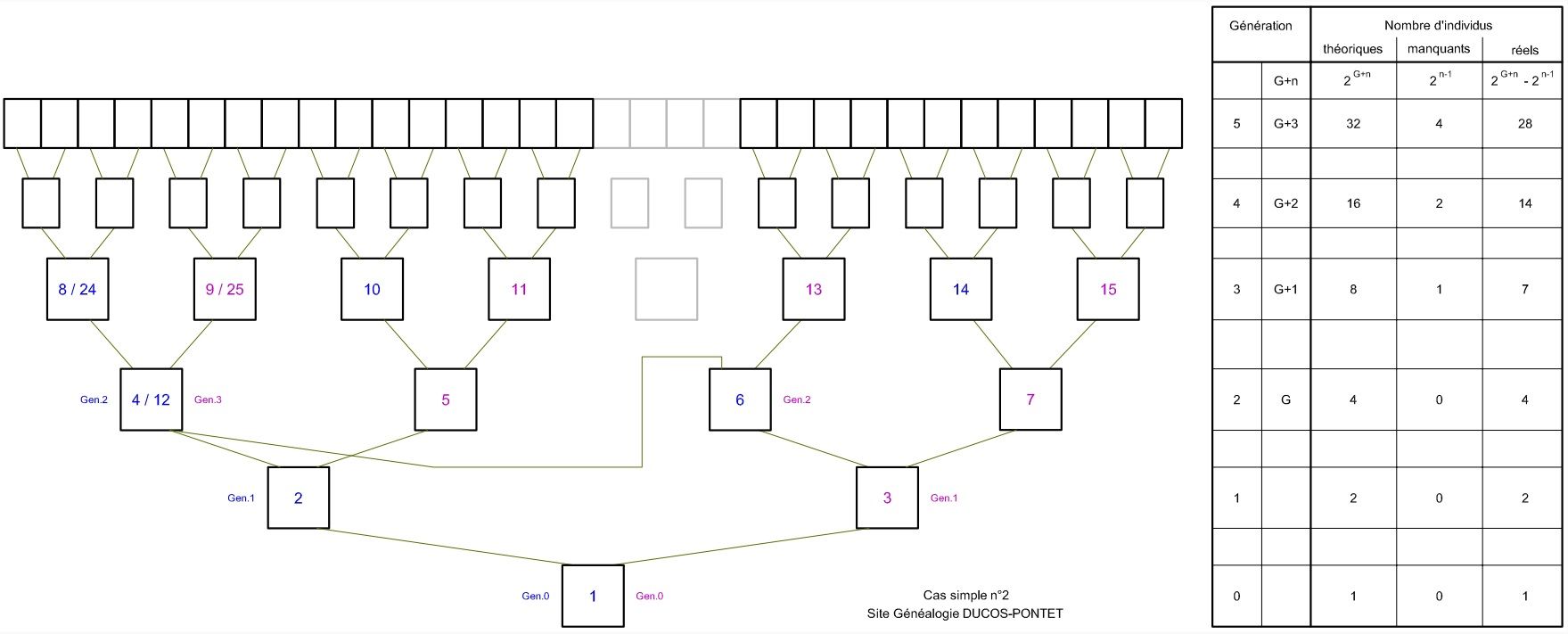
Implexe 2

Résultats constatés :

  • la Gen2 (G) est complète, et la Gen3 (G+1) a 1 seul individu de moins. Si on compte à la GenG+2, on en a 2 de moins. A la GenG+3, on en a 4 de moins. Les manquants doublent à chaque génération.
  • la GenG est toujours complète (2 G), la GenG+1 compte 1 individu de moins (2 G+1 -1).

Conclusions :

  • A la GenG+n, on a 2n-1 manquants.
  • La GenG+n compte donc (2G+n - 2n-1) individus, excepté bien sûr pour la GenG.

Cas concret dans notre généalogie :

Cas simple n°3 : implexage avec fratrie de la même génération :

Cette fois-ci, les ancêtres qui ont les mêmes parents sont le 5 et le 6, qui sont de la même génération. La génération G est la 3, puisque c'est là qu'apparaissent les implexes, leurs parents communs. A la génération Gen3, on a donc 2 implexes (10/12 et 11/13) parents des 2 ancêtres (frères, sœurs ou frère et sœur) de la Gen2, qui prennent la place de 4 individus : les parents du frère et les parents de la soeur.

 

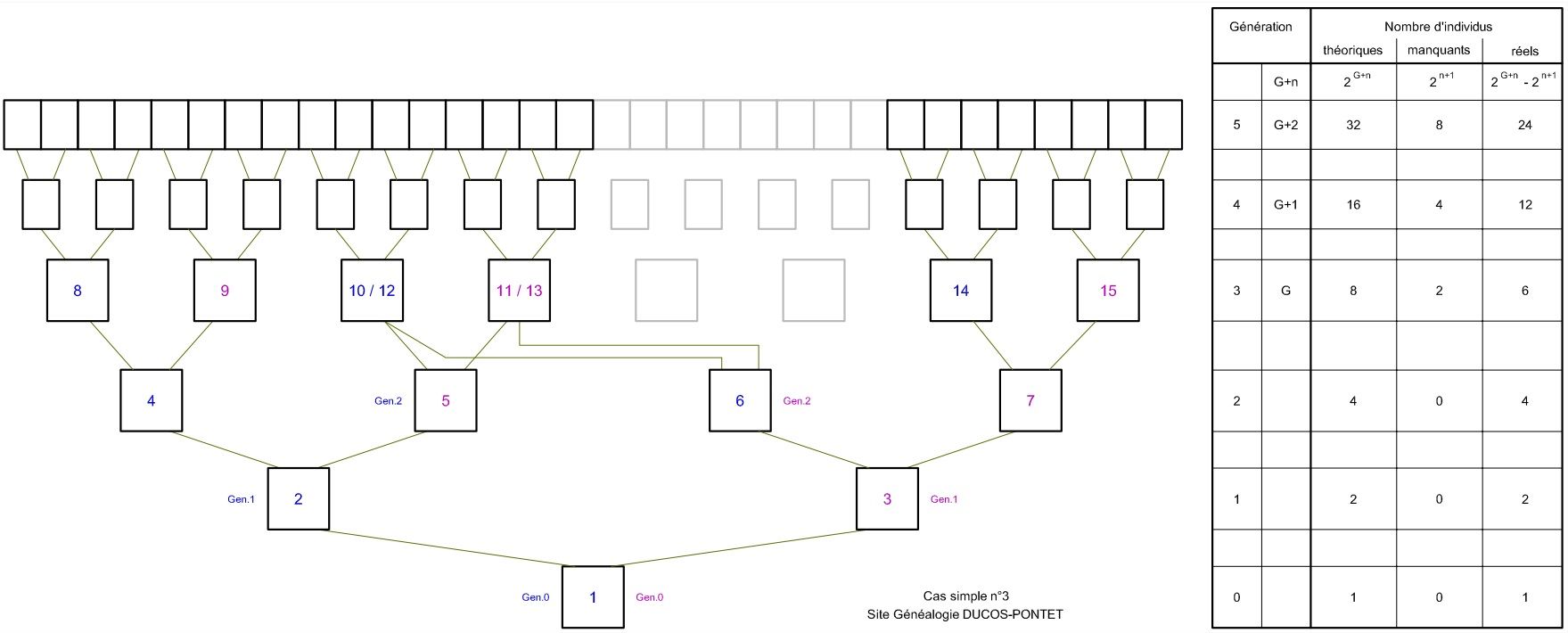
Implexe 3

Résultats constatés :

  • la Gen3 (G) a 2 individus de moins (les enfants ont 2 parents au lieu de 4), puis les manquants doublent à chaque génération.
  • Si on a un implexe à la génération G, la GenG compte 2 individus de moins (2 G -2).

Conclusions :

  • A la GenG+n, on a 2 n+1 manquants.
  • La GenG+n compte donc (2 G+n - 2 n+1) individus.

Cas concret dans notre généalogie :

Cas simple n°4 : implexage sur 2 générations successives :

Reprenons le cas précédent, mais cette fois-ci, nous ajoutons un cas d'implexe à la génération au-dessus. Un cas d'implexage se répète alors sur 2 générations successives : la Gen3 et la Gen4. L'un des parents implexes (10/12) a une soeur (9 dans ce cas ci-dessous, mais ce peut être un frère) qui est aussi un ancêtre. Leurs parents à eux se retrouvent donc avec 3 numéros sosa (18/20/24 et 19/21/25).

 

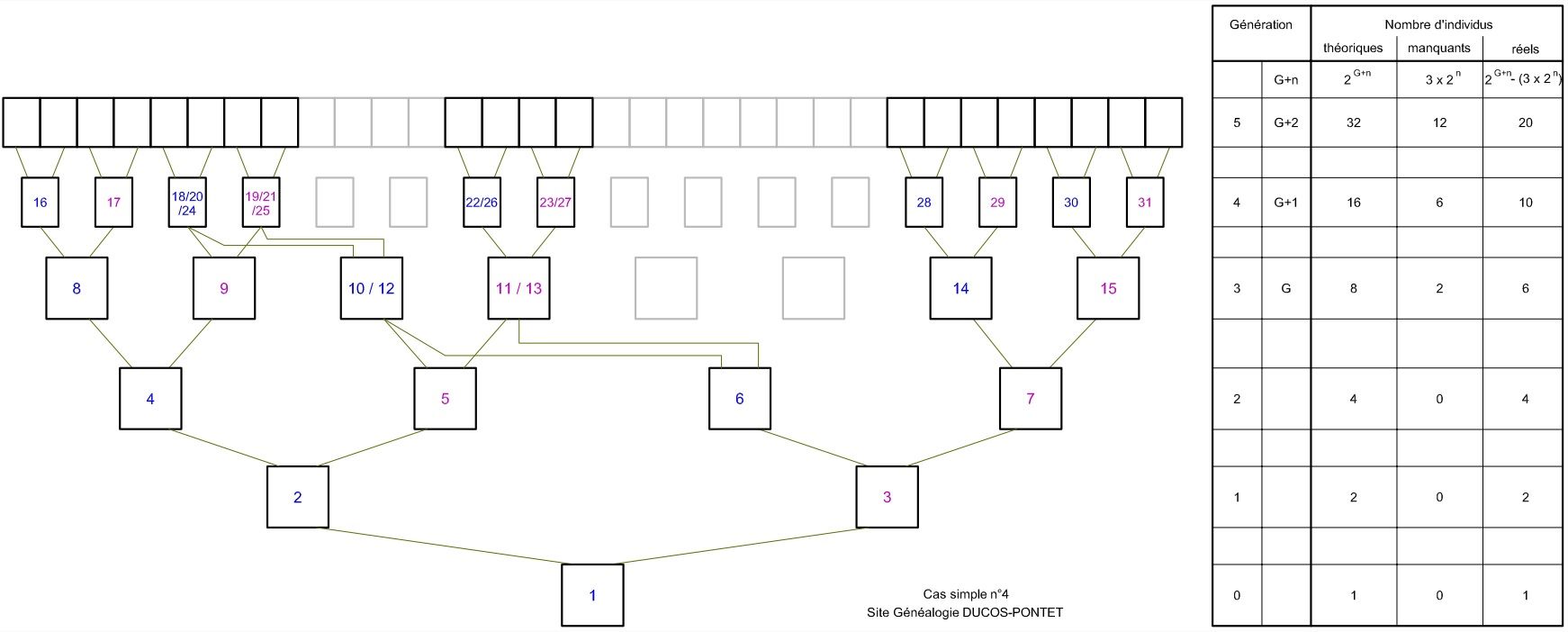
Implexe 4

 

Résultats constatés :

  • La Gen3 (G) a 2 individus de moins, mais la Gen4 (G+1) a les 4 attendus en moins, ainsi que les 2 parents d'un des implexes de la Gen2. Les manquants doublent ensuite à chaque génération.
  • Comme le cas concerne 2 générations successives, on ne peut pas définir de règle mathématique qui marche sur la GenG et sur les suivantes à la fois. La règle ne peut marcher qu'à partir de la GenG+1 et les suivantes.

Conclusions :

  • Pour la GenG, on a toujours 2 manquants. A partir de la GenG+n, on a 3 x 2 n manquants.
  • La GenG+n compte donc (2 G+n - (3 x 2 n)) individus.

Cas concret dans notre généalogie :

  • Aucun. Mais c'est un cas de base général qu'on retrouvera plus loin, avec d'autres subtilités en plus, sinon c'est pas rigolo !

Nous avons vu jusque-là des cas relativement simples. Mais toutes les situations que l'on peut rencontrer ne sont pas forcément aussi faciles à comprendre et à traiter. Que se passe-t-il si plusieurs de ces cas simples sont imbriqués et combinés ? Voici 3 exemples un peu plus complexes.

 

Cas complexe n°1 : 2 implexages sur 2 générations successives, mais le 2ème sur un seul parent commun, avec chaque fratrie de la même génération :

Ce cas découle à la fois des cas simples n°2 et n°4. Dans la Gen3, l'un des parents implexes (10/12) n'a pas une soeur, mais une demi-soeur (9) ! Si vous comparez l'arbre ci-dessous avec celui du cas ci-dessus, vous constatez facilement que la différence se situe au niveau d'un des parents (ici la mère 21/25) de l'implexe demi-frère (10/12).

 

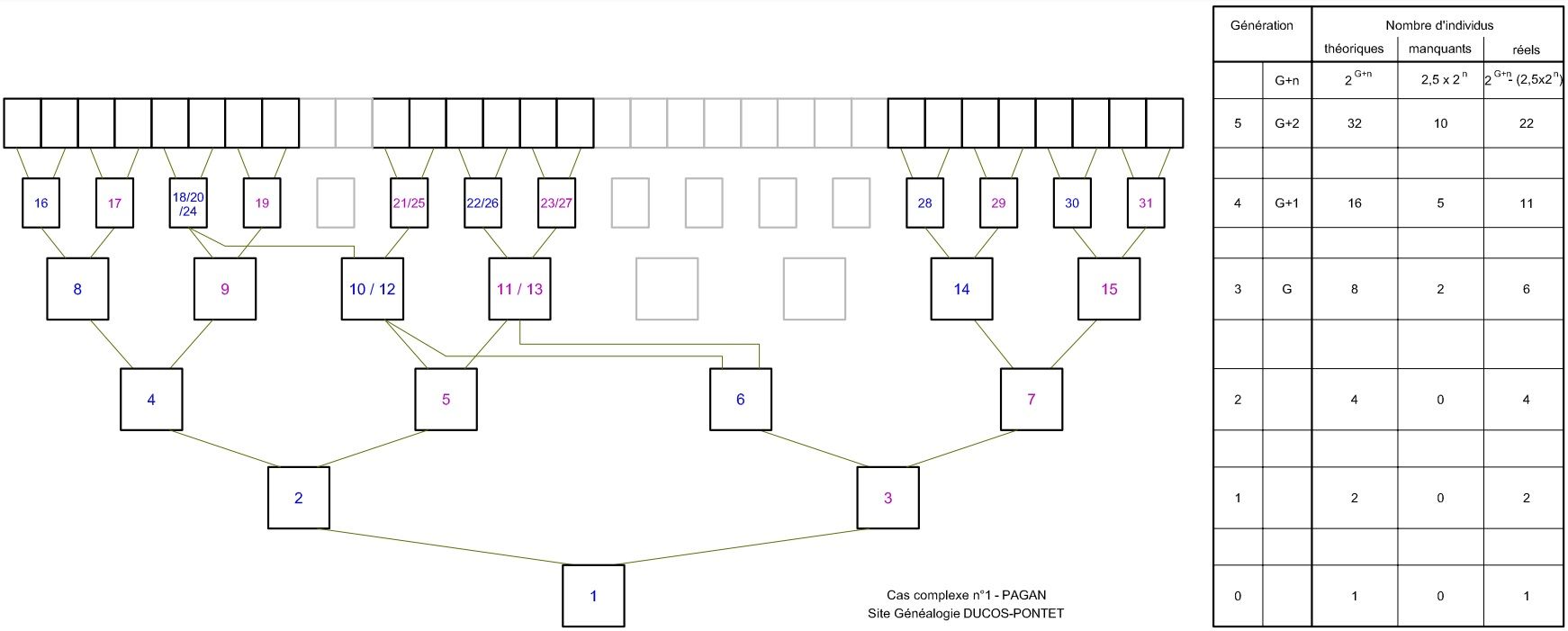
Implexe 4

Résultats constatés :

  • A la Gen3, il manque toujours 2 individus. Mais à la Gen4, il en manque 5. A la Gen5, il en manque 10. Les manquants doublent ensuite à chaque génération.
  • Si on a un implexe à la GenG qui a un frère ou une soeur ancêtre aussi, mais n'impliquant qu'un seul de leurs parents à la GenG+1 comme triple implexe, la GenG compte 2 individus de moins (2 G -2), mais la GenG+1 en compte 5 de moins (2 G+1 -5), la GenG+2 en compte 10 de moins (2 G+2 -10).

Conclusions :

  • Excepté à la GenG, à la GenG+n, on a 2,5 x 2 n manquants.
  • La génération G+n compte donc (2 G+n - (2,5 x 2 n)) individus.

Cas concret dans notre généalogie :

Cas complexe n°2 : implexage sur 3 générations :

Ici, on a d'abord un cas classique d'implexe qu'on a déjà étudié au cas simple n°3, avec 2 ancêtres de la même génération, soeur et frère (5 et 6). A la Gen3, l'un des parents implexes (10/12) a un frère (28) et une soeur (31) qui sont aussi des ancêtres, mais à la génération précédente. A la Gen4, leurs parents à eux se retrouvent donc avec 4 numéros sosa (20/24/56/62 et 21/25/57/63). Enfin, l'un de ces parents (20/24/56/62) a un frère aussi ancêtre (16). Leurs parents à eux, à la Gen5, ont donc 5 numéros sosa (32/40/48/112/124 et 33/41/49/113/125) ! C'est une situation complexe, mais qui se comprend assez bien en regardant l'arbre ci-dessous :

 

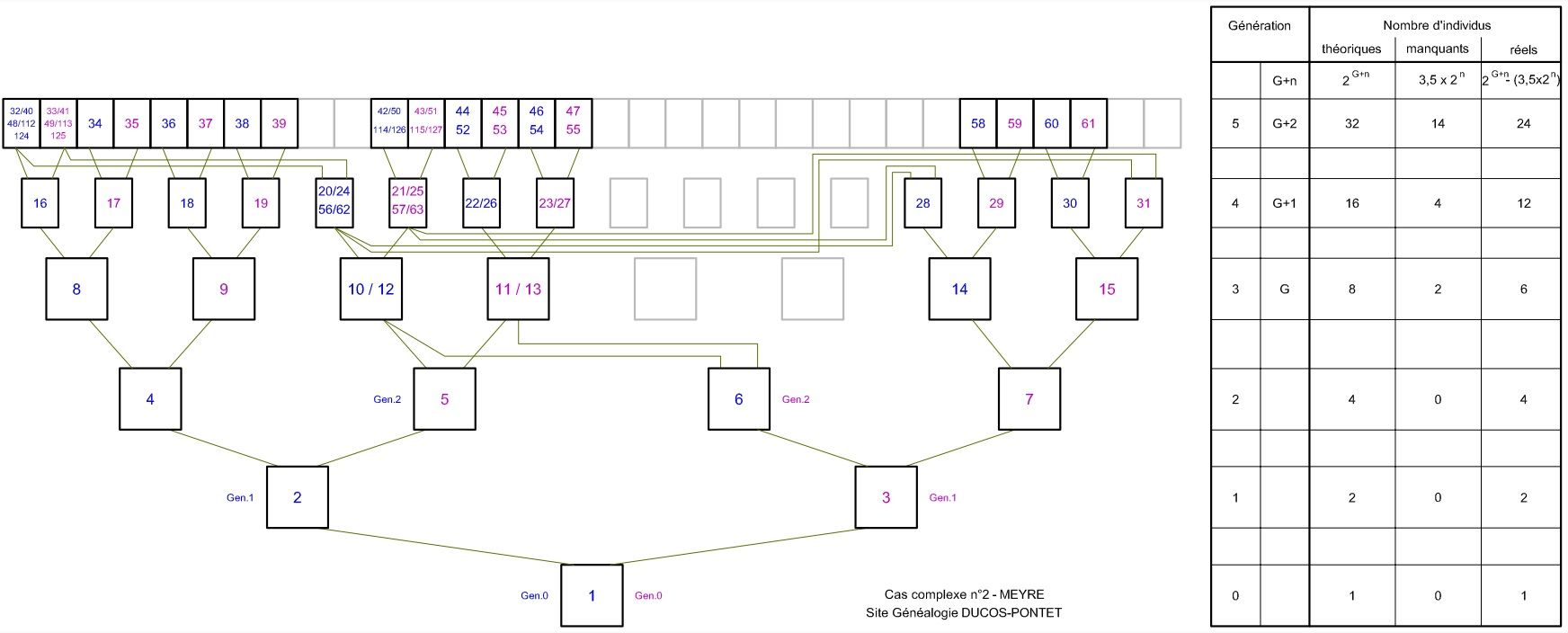
Implexe 5

Résultats constatés :

  • A la Gen3, il manque toujours 2 individus. A la Gen4 (G+1), il ne manque que les 4 parents puisque les frère et soeur qui sont cause de l'implexage de la Gen4 se trouvent eux aussi sur la Gen4. Leurs parents manquants seront donc sur la Gen5. Justement, à la Gen5 (G+2), il en manque 14 (les 8 issus de la Gen3, les 4 issus de la Gen4, et les 2 apparaissant à la Gen5). A partir de la Gen6, les manquants doublent à chaque génération.
  • Dans ce cas aussi, la GenG compte 2 individus de moins (2 G -2), la GenG+1 en compte 4 de moins (2 G+1 -4), la GenG+2 en compte 14 de moins (2 G+2 -14). Dans ces 3 générations où se produisent des implexes, on ne peut pas tirer de formule mathématique qui fonctionne, car les résultats sont modifiés par les nouveaux cas qui arrivent aux générations supérieures.

Conclusions :

  • Sauf entre la GenG et la GenG+1, à la GenG+n, on a 3,5 x 2 n manquants.
  • La génération G+n compte donc (2 G+n - (3,5 x 2 n)) individus.

Cas concret dans notre généalogie :

Cas complexe n°3 : 4 implexages (exemple PAGAN-MEYRE) :

Pour les courageux qui sont arrivés jusqu'ici (bravo à vous !), voici un dernier exemple qui n'est ni plus ni moins que l'exemple le plus complexe que j'ai rencontré. Il s'agit de la situation rencontrée dans le cas imbriqué PAGAN-MEYRE, que vous retrouverez dans la page Nos Implexes, paragraphe MEYRE. Préparez l'aspirine ! Ce cas réel est un mix du cas complexe n°1 (PAGAN) et du cas complexe n°2 (MEYRE). Dans le schéma ci-dessous, tous les individus (frère, soeur, père, mère) sont des ancêtres, et entraînent un implexage sur la génération au-dessus. Les colatéraux n'entrant pas en ligne de compte, ils ne sont pas représentés ici. Dans ce cas, la GenG est la Gen11.

 

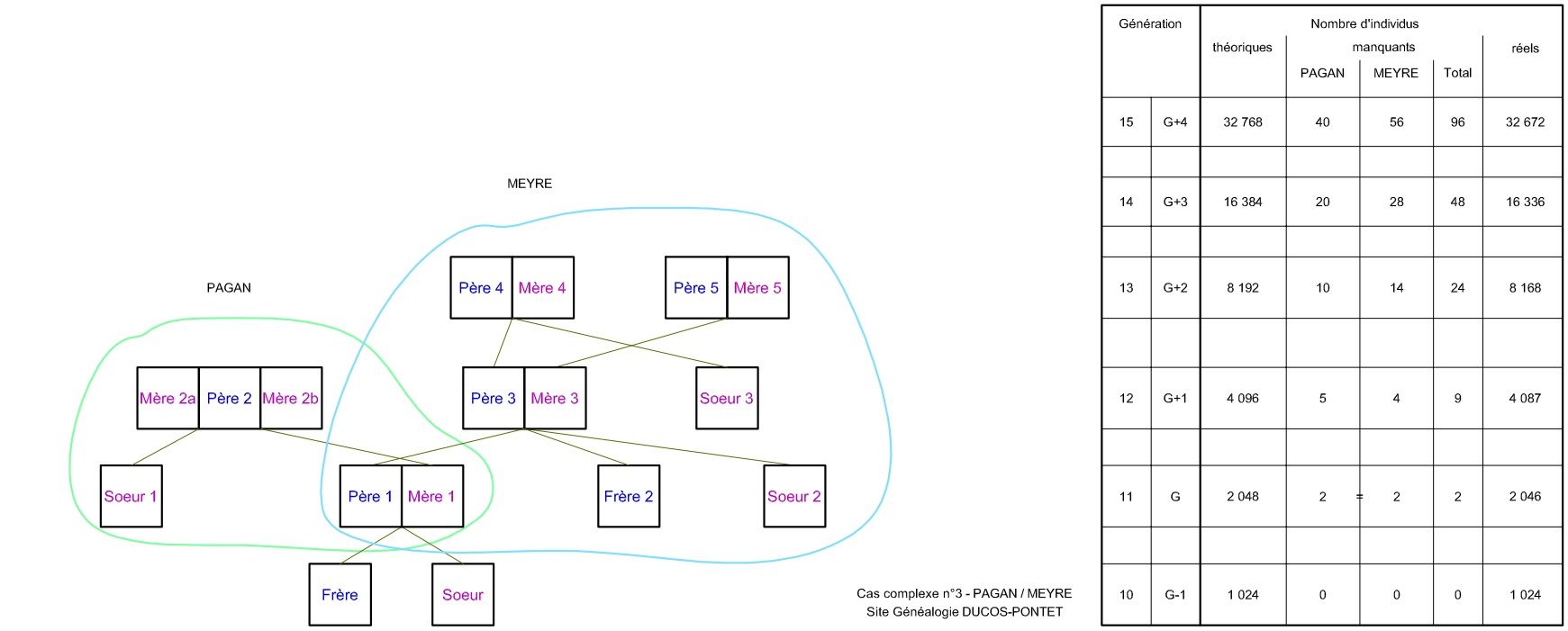
Implexe 6

 

Résultats constatés :

  • J'ajoute les manquants trouvés pour la partie PAGAN avec ceux trouvés pour la partie MEYRE, et ce par génération. Je peux le faire simplement car dans les 2 cas, la GenG est celle où apparaissent les premiers implexes (ici notés Père 1 et Mère 1), qui sont communs aux 2 branches PAGAN et MEYRE, soit la Gen11.
  • Mais pour la GenG précisément, je n'ajoute pas les 2 manquants de PAGAN et les 2 manquants de MEYRE, puisque c'est un seul et même cas commun aux familles. Il ne manque donc que 2 individus en tout.

Conclusions :

  • De la GenG à la GenG+2, on ne peut pas trouver de formule mathématique pour compter les ancêtres manquants puisque la "logique" change en remontant d'une génération, mais à partir de la GenG+2 les manquants doublent à chaque génération. A la GenG+n, on a donc 3 x 2 n+1 manquants.
  • La génération G+n compte donc (2 G+n - (3 x 2 n+1)) individus.

Cas concret dans notre généalogie :

Tout ceci est donc une présentation théorique de différents cas d'implexes dont l'étude est basée sur des cas réels. Mais après la théorie vient enfin la pratique ! Vous pouvez retrouver tous ces cas dans des applications concrètes et bien réelles découvertes dans notre histoire familiale, dans la page "Les implexes dans notre généalogie".

 

 

Aller vers :        Les implexes dans notre généalogie